Задача 1

     В комнате длиной L и высотой H висит на стене плоское зеркало. Человек смотрит в зеркало, находясь на расстоянии l от стены, на которой оно висит. Какова должна быть минимальная высота h зеркала, чтобы он мог увидеть в нем изображение стены, которая находится у него за спиной, во всю ее высоту?

Решение:

     Чтобы решить эту задачу, необходимо выполнить чертеж. Изобразим комнату abcd и зеркало mn на стенке (рис.) Будем считать, что зеркало висит посередине стены, т. е. на одинаковом расстоянии от пола и потолка. Правда, нам об этом ничего не сказано, но такое допущение вполне правомерно. Если же мы его не сделаем, то значительно усложним решение, хотя ответ будет тот же.

     Пусть глаз наблюдателя находится в точке М. Чтобы наблюдатель мог видеть изображение стены ad во всю ее высоту, нужно, чтобы луч, идущий из точки а, отразившись от верхнего края mзеркала mn, попал в глаз наблюдателя, а зеркала mn тоже попал в глаз наблюдателя, расположенный в точке М (см. рис.). При этом нужно помнить, что угол падения луча на зеркало a равен углу его отражения b. Если зеркало расположено симметрично относительно пола и потолка, то эти углы для лучей amи dn одинаковы. Отрезки em и fn на рис. – это перпендикуляры, проведенные к зеркалу в точки падения лучей am и dn на него.

Рис.

     В результате построения мы получили подобные треугольники ame и mMp (они подобны потому, что у них углы при точках е и р – прямые, а углы emp и mMp равны, как накрест лежащие при параллельных em и Mp и секущей Mm). Из подобия треугольников ame и mMp вытекает пропорциональность сторон, лежащих против равных углов:

где, em=L, mp=h/2 и Mp=l (см. рис. 1) Тогда

или

     Отсюда несложно отыскать искомую высоту зеркала h. Выполним простые алгебраические преобразования и найдем ее: H-hl=hL, Hl=h(l+L), откуда

     Задача решена.

Задача 2

     Луч света падает на горизонтальную поверхность стола ab под углом a (рис. а). Под каким углом j к поверхности стола нужно расположить плоское зеркало, чтобы отраженный от него луч стал параллельным поверхности стола?

Решение:

     Выполняя чертеж,нужно учесть следующее:

а) что направление падающего луча не изменится от того, что мы поднесем к столу зеркало;

б) что отраженный от зеркала луч может пойти параллельно поверхности стола влево и вправо в зависимости от того, как мы поднесем к столу зеркало, и при этом углы между зеркалом и столом будут разными, поэтому эта задача имеет два решения.

     Итак, выполним сначала чертеж (рис. а и б).

Рис.

     ab – поверхность стола;

     mn – плоское зеркало, поднесенное к нему под искомым углом j;

     cn – падающий луч (понятно, что это только часть падающего луча, а сам он исходит из некоторого источника, который на рис. не обозначен);

     en – перпендикуляр, опущенный в точку падения n луча к поверхности стола;

     dn – перпендикуляр, опущенный к поверхности зеркала mn в точке n;

     nf – отраженный луч (точнее его часть);

     a₁ – угол падения луча cn на зеркало mn;

     b₁ – угол отражения луча nf от зеркала;

     a – угол падения луча cn на поверхность стола ab;

     j – угол между зеркалом mn и поверхностью стола.

     Анализируя рис.а можно заметить, что сторона mn угла j перпендикулярна стороне dn угла end, а сторона an> угла j перпендикулярна стороне en угла end. Значит, угол j равен углу end как углы со взаимно перпендикулярными сторонами. Из чертежа (рис. а) следует, что угол end равен a₁ –a. Значит, и j=a₁ –a. Но угол a₁ –a, в свою очередь равен a₁ –a=90°-b₁, где угол отражения b₁ по закону отражения равен углу падения a₁, поэтому a₁ –a=90°-a₁, откуда 2a₁=90°+aи a₁=45°+0,5a.

     Тогда j=a₁ –a=45°+0,5a–a, j=45°–0,5a.

     Теперь обратимся к рисунку б. Из этого рисунка следует, что сторона mn угла j перпендикулярна по построению стороне dn угла dne, а сторона nb угла j перпендикулярна по этой же причине стороне en этого же угла dne. Значит, угол j равен углу dne как углы со взаимно перпендикулярными сторонами. Но из рис.б следует, что угол dne равен a₁ +a, значит, искомый угол j=a₁ +a.

     Далее найдем неизвестный угол a₁. Для этого обратим внимание на то, что угол a₁ +a равен a₁ +a=90°-b₁, где по закону отражения b₁=a₁, поэтому a₁ +a=90°-a₁, 2a₁=90°-a и a₁=45°–0,5a. Но тогда j=a₁ +a=45°–0,5a+a, j=45°+0,5a.

     Задача решена.

Задача 3

     Определите, на какой угол q отклоняется световой луч от своего первоначального направления при переходе из воздуха в воду, если угол падения a=75°.

Решение:

     Из рис.  видно, что q=a-b.

     Рис.

     Согласно закону преломления       где n – показатель преломления воды. Отсюда

     Из таблицы синусов находим для b: b»46°33¢.

     Следовательно, q=75°-46°33¢»28°27¢

     Задача решена.

Задача 4

     Начертите ход лучей сквозь треугольную стеклянную призму, основанием которой является равнобедренный прямоугольный треугольник. Лучи падают на широкую грань перпендикулярно этой грани.

Решение:

     Проходя через широкую грань, лучи своего направления не изменяют, так как угол падения равен нулю (рис.). На узкой грани лучи претерпевают полное отражение, так как угол падения равен 45° и, следовательно, больше предельного угла полного отражения для стекла. После полного отражения от левой грани лучи падают на правую грань, вторично претерпевают полное отражение и выходят из призмы по направлению, перпендикулярному широкой грани. Таким образом, направление пучка света изменяется в данном случае на 180°. Такой ход лучей используется, например, в призматических биноклях.

     Рис.

     Задача решена.

Задача 5

     Определите, во сколько раз истинная глубина водоема больше кажущейся, если смотреть по вертикали вниз.

Решение:

     Построим ход лучей, вышедший из точки S на дне водоема и попавших в глаз наблюдателя (рис.). Так как наблюдение ведется по вертикали, один из лучей SA направим перпендикулярно поверхности воды, другой SB – под малым углом a к перпендикуляру. (При больших углах a лучи не попадут в глаз.) После преломления на поверхности воды лучи идут расходящимся пучком. Вершина этого пучка представляет собой мнимое изображение S₁ точки S.

Рис.

     Угол ASB равен углу падения a (как внутренние накрест лежащие), а угол AS₁B равен углу преломления b (как соответственные при параллельных).Прямоугольные треугольники ASB и AS₁B имеют общий катет AB, который можно выразить через истинную глубину водоема SA=H или через кажущуюся глубину S₁A=h:

AB=Htga=htgb.

     Отсюда

     Так как углы a и b малы, то

     Следовательно,

     Истинная глубина водоема больше кажущейся в n =1,3 раза.

     Задача решена.

Задача 6

     Плоское зеркало повернули на угол a=17° вокруг оси, лежащей в плоскости зеркала. На какой угол b повернулся отраженный луч, если направление падающего луча осталось неизменным?

Решение:

     Пусть j - первоначальный угол падения луча (рис.). По закону отражения угол отражения также равен j, и, следовательно, угол между падающим лучом и отраженным лучом равен 2j. При повороте зеркала на угол a перпендикуляр к зеркалу, восстановленный в точке падения, также повернется на угол a. Поэтому новый угол падения будет равен j+a. Таким же будет и новый угол отражения. Поэтому угол между лучом падающим и лучом отраженным станет равным 2(j+a), т. е. изменится по сравнению с прежним на 2a. Следовательно, отраженный луч повернется на угол b=2a=34°.

Рис.

     Задача решена.

Задача 7

     В опыте Юнга по дифракции расстояние между щелями d=0,07 мм, а расстояние от двойной щели до экрана D=2м. При освещении прибора зеленым светом расстояние между соседними светлыми дифракционными полосами оказалось равным Dh=16 мм. Определите по этим данным длину волны.

Решение:

     В некоторой точке С экрана (рис.) будет наблюдаться максимум освещенности при выполнении условия d₂-d₁=kl, где k=0, 1, 2,… - целые числа.

     Рис.

     Применим теорему Пифагора к треугольникам S₁CE и S₂CB:

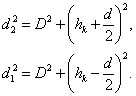
     Вычитая почленно из первого равенства второе, получаем или (d₁+d₂)(d₂-d₁)=2h_kd.

     Так как d<<D, то d₁ +d₂»2D. Следовательно,

     Отсюда находим расстояние k-й светлой полосы от центра экрана:

     Расстояние между соседними полосами равно:

     Отсюда

     Учитывая, что d₂-d₁=kl, можем записать

     Задача решена.

Задача 8

     На дифракционную решетку, имеющую 500 штрихов на миллиметр, падает плоская монохроматическая волна (l=5×10^-5см). Определите наибольший порядок спектра k, который можно наблюдать при нормальном падении лучей на решетку.

     Максимальному k соответствует sinj=1. Следовательно,

     Задача решена.

Задача 9

     Два плоских зеркала расположены под углом друг к другу. Точечный источник света расположили между ними, и в результате получили n=11 изображений этого источника в зеркалах. Чему равен угол a между зеркалами?

Решение:

     Если построить все изображения, то чертеж получится чрезмерно усложненным, поэтому мы не станем здесь его вычерчивать, а ограничимся напоминанием основных правил построения изображения в таких зеркалах:

     а) изображение точечного источника света в плоском зеркале мнимое;

     б) оно располагается на таком же расстоянии от зеркала, что и сам предмет;

     в) изображение предмета является прямым и равным по размерам самому предмету;

     г) изображение, даваемое одним из зеркал, расположенных под углом друг к другу, является предметом для второго зеркала, а изображение, даваемое вторым зеркалом, - предметом для первого зеркала и т. д.

     Если два плоских зеркала расположены под углом a друг к другу, то число изображений n предмета, помещенного между ними, определяет формула

     Из этой формулы несложно отыскать искомый угол a между зеркалами, поскольку число изображений n нам известно из условия задачи,

откуда

     a=30°

     Задача решена.

Задача 10

     Каков период d решетки, если при нормальном падении на нее лучей с длиной волны l=0,75 мкм на экране, отстоящем от решетки на расстоянии L=1 м, максимумы первого порядка (k=1) отстоят друг от друга на х=30,3 см? Каково число штрихов N на l=1 см решетки? Какое количество m максимумов дает эта дифракционная решетка? Каков максимальный угол j_max отклонения лучей, соответствующих последнему дифракционному максимуму?

Решение:

     Постоянная решетки d может быть найдена из условия максимума на решетке:

d×sinj=kl,

где k=1, т. к. в условии говорится о максимумах первого порядка, j - угол дифракции лучей, образующих максимум первого порядка.

Рис.

     Так как по условию во много раз меньше L, то sinj»tgj. Из рис. видно, что

     Тогда:

     или        

     Зная d, можно найти, сколько периодов (а значит, и сколько штрихов) укладывается на единице длины решетки.

     Поскольку

  то   

     Для определения порядка последнего максимума надо учесть, что максимальный угол отклонения лучей после прохождения через дифракционную решетку не может превышать 90°. Тогда из условия главных максимумов

 или  

     Общее число максимумов m, даваемых дифракционной решеткой,

m=2k_max+1,     

(такой результат получается, если учесть центральный максимум и то, что влево и вправо от него расположены по k_max максимумов).

     Максимальный угол отклонения лучей, соответствующих последнему дифракционному максимуму, определяется из соотношения

   и   

     d=4,95×10^-6м, N/l=2,02×10³1/см, m=13, j_max=65°

     Задача решена.